关于 光栅化(rasterrization) 中的 DDA 与 Bresenham 两种算法
光栅化
首先我们要明白一些常识: 计算机是如何显示图像的?
答案很简单, 用电子枪发射电子, 通过电磁场偏转来控制其方向, 打在屏幕上, 进行高速扫描(scan), 即电子束从左往右, 从上往下发射
只要在短时间内多次进行扫描, 利用人眼的视觉暂留效果, 让图像, 即上色的像素集合 "显示" 出来
RGB 三原色, 位深分别为 8bit, 即 1byte, 就能构成 (2^8^ * 2^8^ * 2^8^) 种组合, 是爆表多的颜色种类啊
只要将一束电子, 变为三束电子, 分别掌管 RGB, 瞄准显示屏上的特定一小块, 就有绚丽多彩的颜色了, 我们称其为, 像素(pixel)
同时, 这里有两个概念要区分一下:
- 片元(fragment): 物理层次上的显示屏上的一小块/一小单元, 概念上更加客观些
- 像素(pxiel): 已经被染色的图片单元, 概念上更高级更抽象些, 以片元为载体
光栅(Raster), 德语中 "屏幕" 的意思, 光栅化自然就是指把什么东西渲染到屏幕上的过程咯
可以简单理解为, 光栅化就是在研究, 在屏幕上绘制像素的过程
下面将介绍两种将直线给光栅化的算法, 不要担心, 难度不大, 只需要初中级别的数学水平即可
并且假设你已经知道for循环, function, 赋值等编程中的基本概念
DDA算法
DDA(Digital Differential Analyzer), 数字微分分析法, 可别被这名字给吓到了, 实际上这是很容易理解的
假设每个像素方块, 其左下角为该像素的坐标, 已知起点与终点的坐标 $\begin{cases}(x_1, y_1)\\(x_2, y_2)\end{cases}$, 可求出其斜率k
当k<1时, 如图所示, x每增加1时, y需要增加m, 随后将y向下取整得到yy, 然后渲染(x, yy):
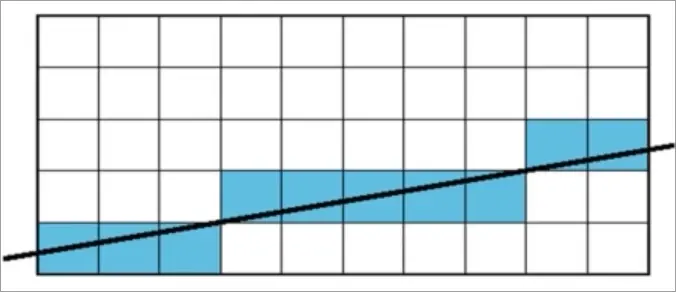
用伪代码表示的话, 就是这样:
for x in x1..=x2 step=1.0
y1 += k
yy = floor(y1) // 关键, 但可以不是floor
write_pixel(x, yy, BLUE)
结合图片, 相信你应该能够看懂
当然, 我们还可以选择不用 floor, 而是 round, 这叫做圆整处理, 可以尽量做到直线平滑
此处, 可以将四舍五入理解为圆整处理, 伪代码如下:
for x in x1..=x2 step=1.0
y1 += k
yy = round(y1) // 圆整处理
write_pixel(x, yy, BLUE)
但还有一些问题, 那就是当斜率k > 1时, 即倾斜角大于 45 度时, 如果按照 "x不断+1, y不断+k" 的套路, 将无法连续, 如下左图所示
此时, 我们就应该反转一下, 按照 "y不断+1, x不断+1/k" 的套路, 才能做到尽量连续, 即反转了x与y轴, 如下右图所示
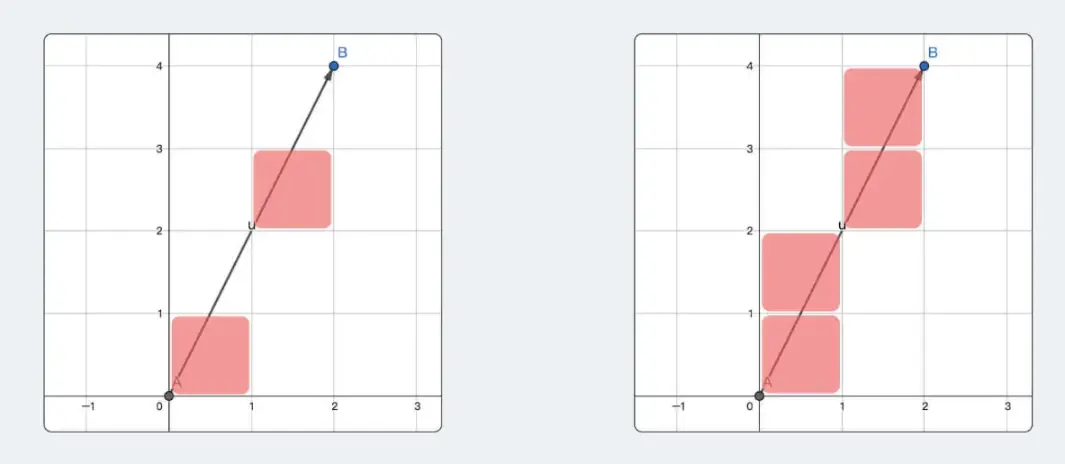
我们将沿着x轴的方向, 或沿着y轴的方向, 移动幅度大的那一个方向, 称作 主位移方向
如上面的图1, x轴为主位移方向, 而在图2中, y轴是主位移方向
当斜率k为负数时, 也可以按照以上两种思路进行处理, 要同时处理正负, 避免if分情况判断的话, 用 abs 计算绝对值即可
完整处理的伪代码如下:
dx = abs(x2 - x1)
dy = abs(y2 - y1)
// 确定主位移方向是x轴还是y轴, 记得要用绝对值来避免对正负讨论
d = max(dx, dy)
// 当主位移方向为x轴, 则按照 "x不断+1, y不断+k", 不然按照 "y不断+1, x不断+1/k"
dxx = dx / d
dyy = dy / d
// 从x1遍历到x2
// 当主位移方向为x轴时, dxx=1, dyy=k
// 当主位移方向为y轴时, dxx=1/k, dyy=1
for x in x1..=x2 step=dxx
y1 += dyy
yy = round(y1) // 圆整处理
write_pixel(x, yy, COLOR)
但还是不够高效, 因为涉及了大量浮点数计算, 比如 y1 += dyy
同时, for 循环那里可能因为浮点计算不够精准, 次数不够准确, 可以改写为遍历 step 次, 然后在循环体内 x += dxx, 但为了美观我懒得改了
